Das Monty-Hall-Problem
Im »Parade Magazine« erscheint eine Kolumne namens »Ask Marylin«. Dort beantwortet Marilyn vos Savant, einer der intelligentesten Menschen der Welt (siehe Wikipedia.de) Leserfragen. Nun kam es 1990 zu folgender Frage:
Angenommen, man ist Kandidat in einer TV-Spielshow und muss sich für eine von drei Türen entscheiden. Hinter zwei Türen versteckt sich jeweils eine Ziege und hinter einer Tür ein Auto. Nun wählt man eine Tür aus und stellt sich vor diese. Da der Moderator weiß, hinter welcher Tür sich was verbirgt, öffnet er eine andere
Tür, hinter der eine Ziege steht, und fragt nun den Kandidaten, ob er bei seiner Türe bleiben oder wechseln will.
Nun fragte der Leserbrief-Verfasser die Kolumnistin, wie er sich in einer solchen Situation verhalten solle. Hätte er einen Vorteil, wenn er sich jetzt doch für die andere Tür entscheiden würde?
Was würdest du sagen?

Lösung:
Was sagt dein Logiksinn? Die meisten werden antworten, dass es völlig egal sei, ob man nun wechselt oder nicht. Wenn hinter einer Tür ein Auto und hinter der anderen eine Ziege steht – dann sei die Chance 50:50.
Aber vos Savant riet, auf jeden Fall zu wechseln, da seine Chancen, das Auto zu gewinnen, dann höher wären. Nach Veröffentlichung kamen hunderte Beschwerde-Briefe von Mathematikern und Professoren im Verlag an – und auch nachdem vos Savant Monate später noch auf die Richtigkeit ihrer Antwort hinwies, kam es zu einer großen Kontroverse.
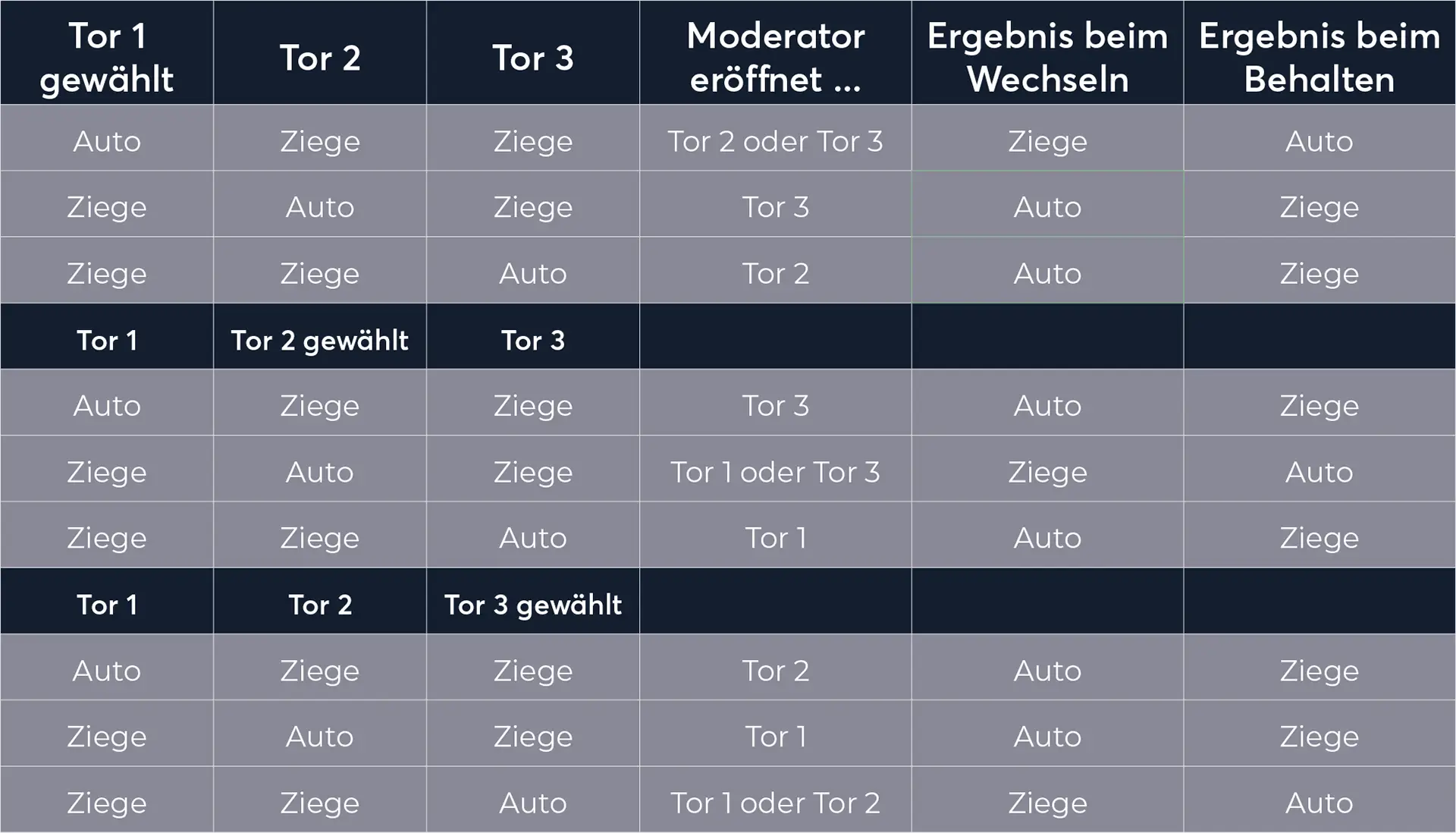
Doch nun das für viele Verblüffende: Marylin vos Savant hat recht. Es gibt dazu einen mathematischen Ansatz, den wohl die wenigsten kapieren. Aber der graphische Ansatz (siehe Bild) macht deutlich, warum man eine 2/3-Chance auf das Auto hat, wenn man wechselt.
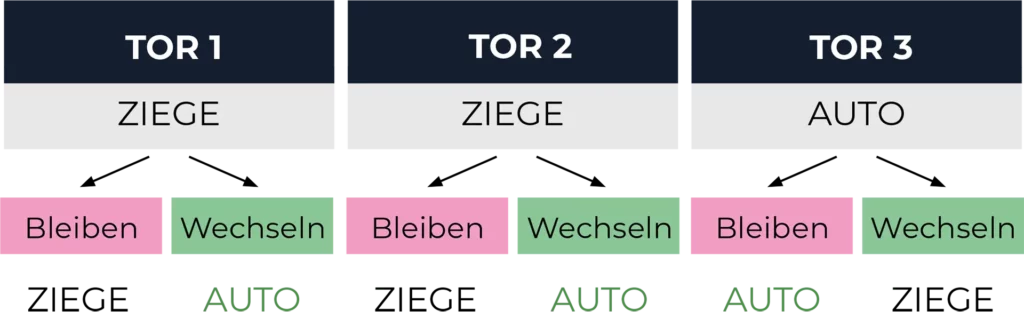
Man sieht hier (von der Startposition ausgehend), dass man, wenn man wechselt, in 2 Fällen das Auto gewinnt und nur in 1 Fall bei der Ziege landet.
Ich weiß, das ist eher ein mathematisches Problem als eine Denksportaufgabe, aber allein dadurch, dass du darüber nachdenkst, aktivierst du dich. Wie ich finde, sind solche Aufgaben auch wunderbar dazu geeignet, uns ab und zu aufzuzeigen, wie verblüffend es sein kann, gedankliche Grenzen einmal zu überschreiten.

Die 66 besten Denksportaufgaben weltweit

